本篇文章参考了labuladong的算法教学，是自己总结的算法学习笔记。
今天我们学习的是利用双指针解决单链表问题, 主要应用分离双指针和快慢指针两种算法.

链表合并&分解

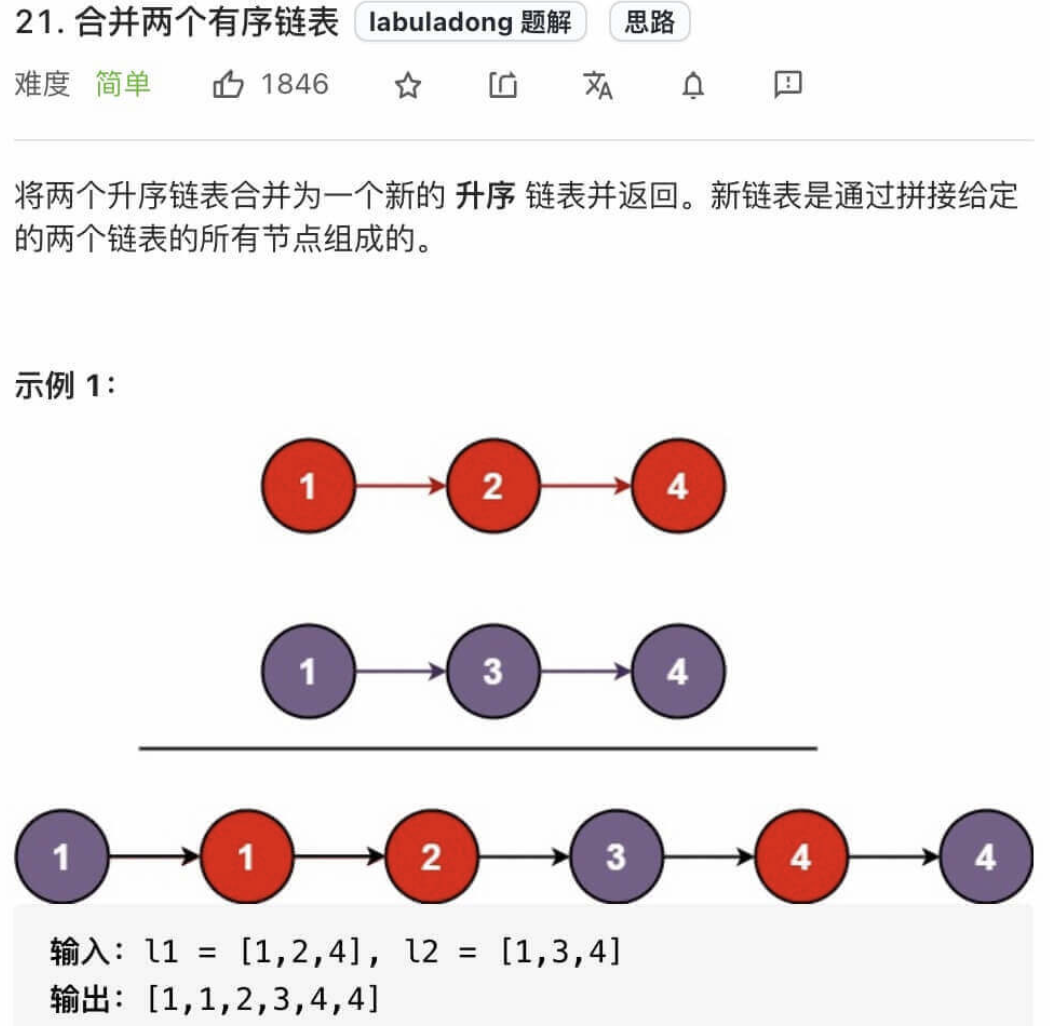
21.合并两个有序链表

class Solution {
public:
	ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
		ListNode * head = new ListNode(-1);
		ListNode * fakeHead = head;
		ListNode * p1 = list1;
		ListNode * p2 = list2;
		
		while(p1 != nullptr && p2 != nullptr){
			if(p1->val < p2->val){
				fakeHead->next = p1;
				p1 = p1->next;
			}else{
				fakeHead->next = p2;
				p2 = p2->next;
			}
			fakeHead = fakeHead->next;
		}
		
		if(p1 != nullptr){
			fakeHead->next = p1;
		}
		
		if(p2 != nullptr){
			fakeHead->next = p2;
		}
		
		head = head->next;
		return head;
	}
};

该问题就是将以数组为存储形式的归并排序问题转化为了以链表为存储形式. 值得注意的一点是在算法中我们使用了一个dummy的伪头结点, 作为形成新链表所需要的表头.
这里就可以看出链表的优势: 节点间的联系是通过指针维持的, 不需要开辟新的空间来存储节点.

也可以不使用dummy节点, 直接使用list1的头结点作为最后的结果头结点, 但需要对空指针进行额外判断:

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(list1 == nullptr) return list2;
        if(list2 == nullptr) return list1;
        ListNode * head;
        ListNode * fakeHead;
        
        if(list1->val <= list2->val){
            head = list1;
            fakeHead = list1;
            list1= list1->next;
        }else{
            head = list2;
            fakeHead = list2;
            list2= list2->next;
        }
        ListNode * p1 = list1;
        ListNode * p2 = list2;
        while(p1 != nullptr && p2 != nullptr){
            if(p1->val < p2->val){
                fakeHead->next = p1;
                p1 = p1->next;
            }else{
                fakeHead->next = p2;
                p2 = p2->next;
            }
            fakeHead = fakeHead->next;
        }
        if(p1 != nullptr){
            fakeHead->next = p1;
        }
        if(p2 != nullptr){
            fakeHead->next = p2;
        }
        head = head->next;
        return head;
    }
};

单链表的分解

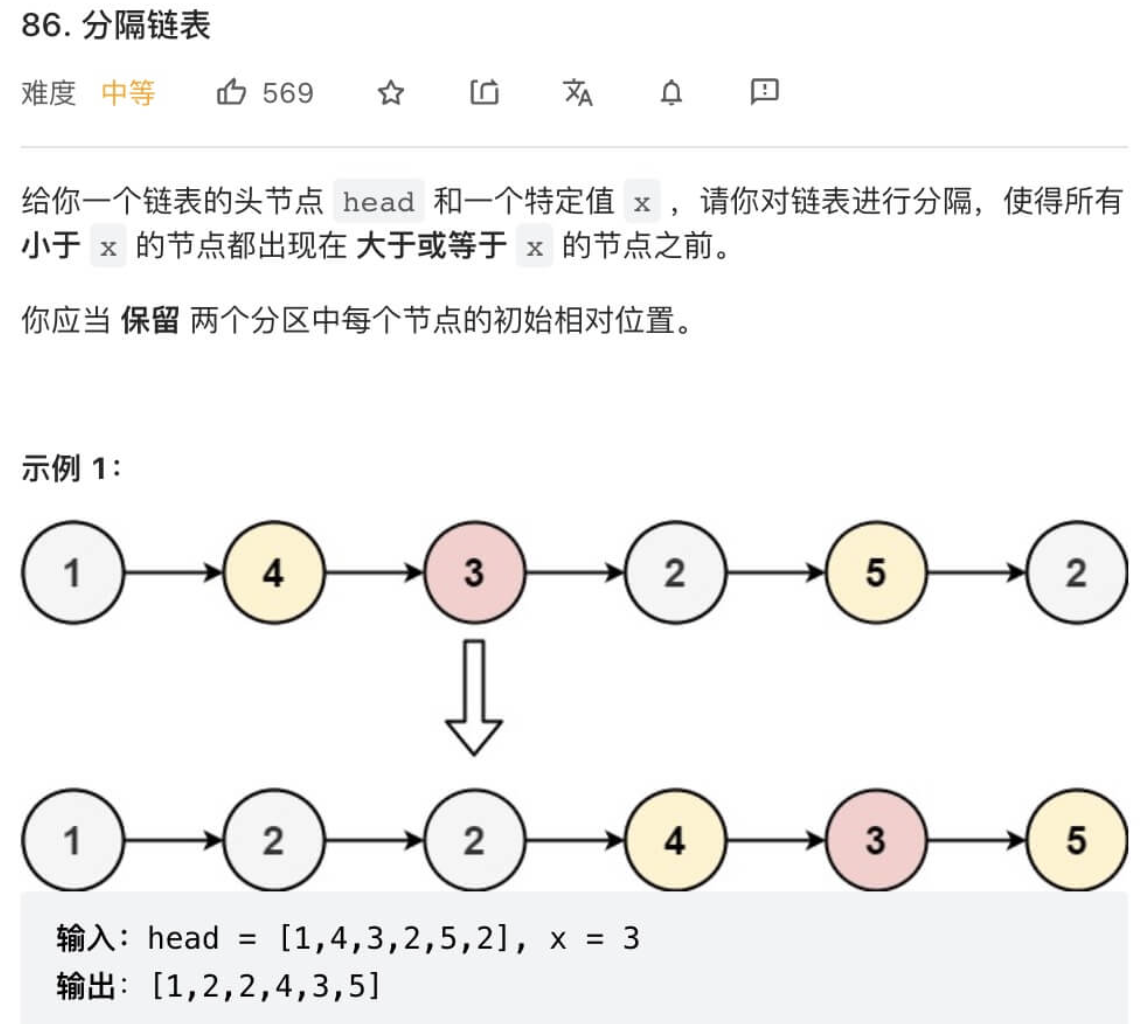
与合并双链表类似, 我们的思路是将一个链表分成两个: 一个保存<x的节点; 另一个保存>=x的节点, 然后将两个链表合并即可得到最终结果:

class Solution {
public:
    ListNode* partition(ListNode* head, int x) {
        ListNode * dummy1 = new ListNode(-1);
        ListNode * dummy2 = new ListNode(-1);
        ListNode * p1 = dummy1;
        ListNode * p2 = dummy2;
        ListNode * p = head;
        while(p != nullptr){
            if(p->val < x){
                p1->next = p;
                p1 = p1->next;
            }else{
                p2->next = p;
                p2 = p2->next;
            }
            ListNode * temp = p->next;
            p->next = nullptr;
            p = temp;
        }
        p1->next = dummy2->next;
        return  dummy1->next;
    }
};

代码的大部分逻辑与合并双链表类似, 同样使用了两个dummy节点来方便操作. 但代码中多了这段内容:

ListNode * temp = p->next;
p->next = nullptr;
p = temp;

这段代码的作用是断开当前节点p与后续节点的联系后让p前进一个节点.
在合并两个链表时, 由于链表是有序的, 且list1和list2之间没有联系, 所以算法一定会对最大值节点外所有节点的next重新赋值, 因此不可能存在环.
但在将一个无序链表分离为两个链表时, 则会有成环的可能: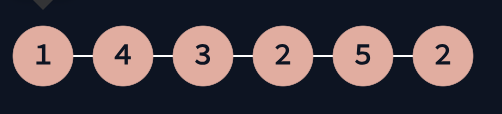

这样的一个链表, 假设x=3.
那么p1的最后一个节点一定是最后一个2;
p2的最后一个节点一定是5.
如果不断开节点间联系, 那么2与5之间会有一个next连接, 此时再将p1和p2所在链表连接会出现环: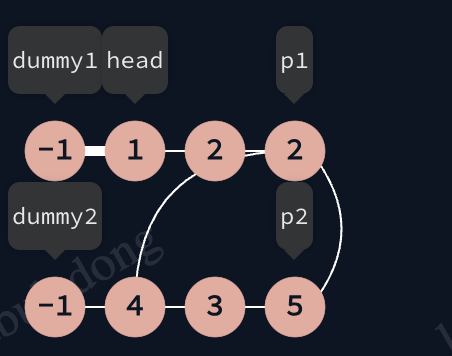

而在单链表中是不允许有环存在的, 会永远无法遍历完链表.
所以, 记住在涉及分离链表节点时:

ListNode * temp = p->next;
p->next = nullptr;
p = temp;

重置next指针很重要!

合并k个有序链表

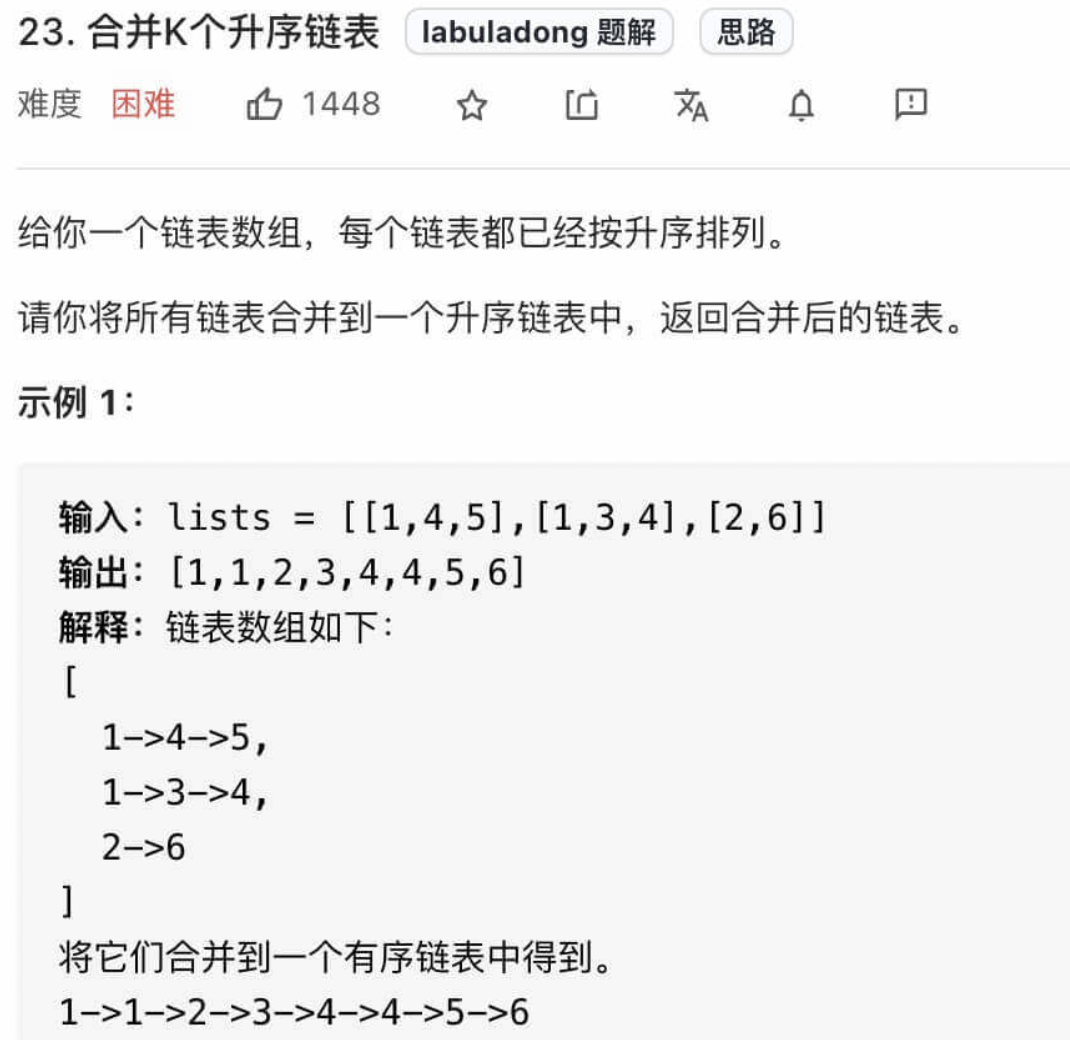
相比合并两个有序链表, 该题目的主要问题在于 如何每次从k个结点中寻找出val最小的节点. 我们想到了使用优先队列来解决该问题:

class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        ListNode* dummy = new ListNode(-1);
        ListNode* p = dummy;
        priority_queue<ListNode*, vector<ListNode*>, function<bool(ListNode*, ListNode*)>> pq([] (ListNode* a, ListNode* b) { return a->val > b->val; });
        for(ListNode* head: lists){
           if(head != nullptr){
               pq.push(head);
           } 
        }
        while(!pq.empty()){
            ListNode* node = pq.top();
            pq.pop();
            p->next = node;
            if(node->next != nullptr){
                pq.push(node->next);
            }
            p = p->next;
        }
        return dummy->next;
    }
};

我们首先将k个链表的表头插入队列, 由于比较函数是greater, 因此优先队列的top()总会是k个元素中最小的.
后续过程中反复将非空的节点加入队列, 直至队列中再无元素即可获得合并后的链表.

链表定位问题

链表虽然在合并分离上有着十分灵活的优势, 但他也有一个问题: 只能顺序读取, 即如果想要得到链表的最后一个节点, 就只能把前面的所有节点都遍历一遍.
因此, 对链表中特点位置的元素进行访问是一个问题.

单链表的倒数第k个结点

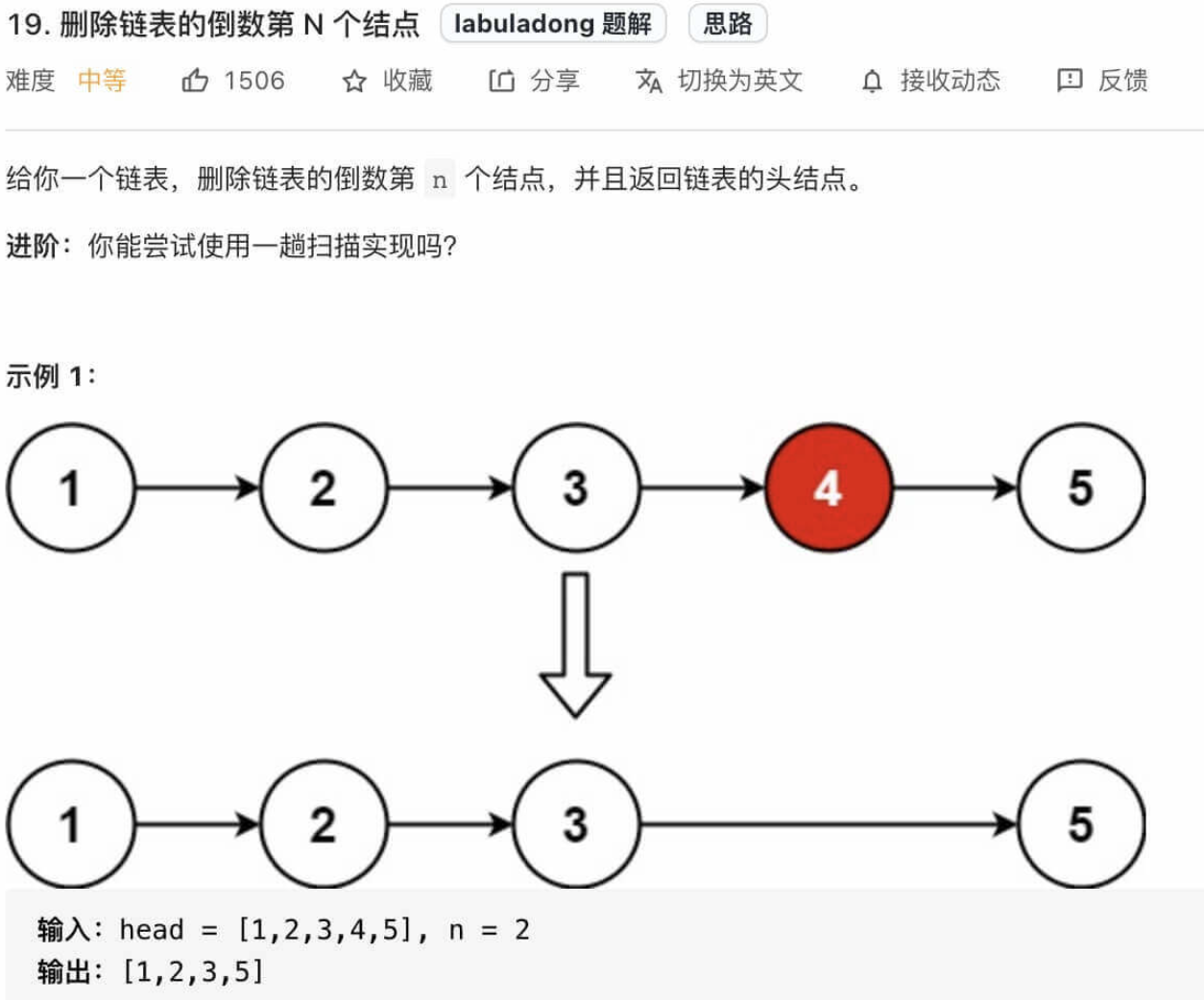
看到问题首先的想法是, 先遍历一遍单链表得到表长度n, 然后倒数第k个结点就是正数第n-k+1个结点, 利用for循环即可. 但这种算法需要遍历两次链表, 是否有办法遍历一次链表呢?

使用快慢指针: 两个指针都指向头结点, 先让一个指针率先前进k个节点, 然后两个指针同步前进, 当快指针为空时, 慢指针就指向了倒数第k个结点.

你会想, 这样对链表的读取次数不还是一样的嘛? 但由于这样的访问方式会有更优的局部性, 所以理论来说速度会更快:

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode(-1);
        dummy->next = head;
        ListNode* p1 = dummy;
        for(int i =0; i<n+1; ++i){
            p1 = p1->next;
        }
        ListNode* p2 = dummy;
        while(p1 != nullptr){
            p1 = p1->next;
            p2 = p2->next;
        }
        p2->next = p2->next->next;
        return dummy->next;
    }
};

单链表的中点

同样地使用两次遍历的思路就是先得到链表长度n, 再计算中间节点位置(n/2)即可.

是否可以再使用双指针的方式通过一次遍历解决该问题呢?

首先让slow和fast指针都指向头节点, 每当slow节点前进一步, fast节点前进两步, 当fast节点走到尽头时 slow节点正好在中点位置:

class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != nullptr && fast->next != nullptr){
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }
};

如果对于偶数长度的链表, 中点事第一个呢?

只需要加一个判断即可:

```cpp
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != nullptr && fast->next != nullptr){
            fast = fast->next->next;
            if(fast == nullptr) break;
            slow = slow->next;
        }
        return slow;
    }
};

链表判环问题

解决该问题也是使用快慢指针的方法:
slow指针每走一步, fast指针走两步, 这样fast在k次操作后会比slow多走k步, 当k为环长度的整数倍时, 两个指针就会相遇.

在判断的存在环的基础上, 有一些更进阶的问题:

环+起点

判断存在环的方式我们已经明白了, 但如果有环, 怎么算起点呢?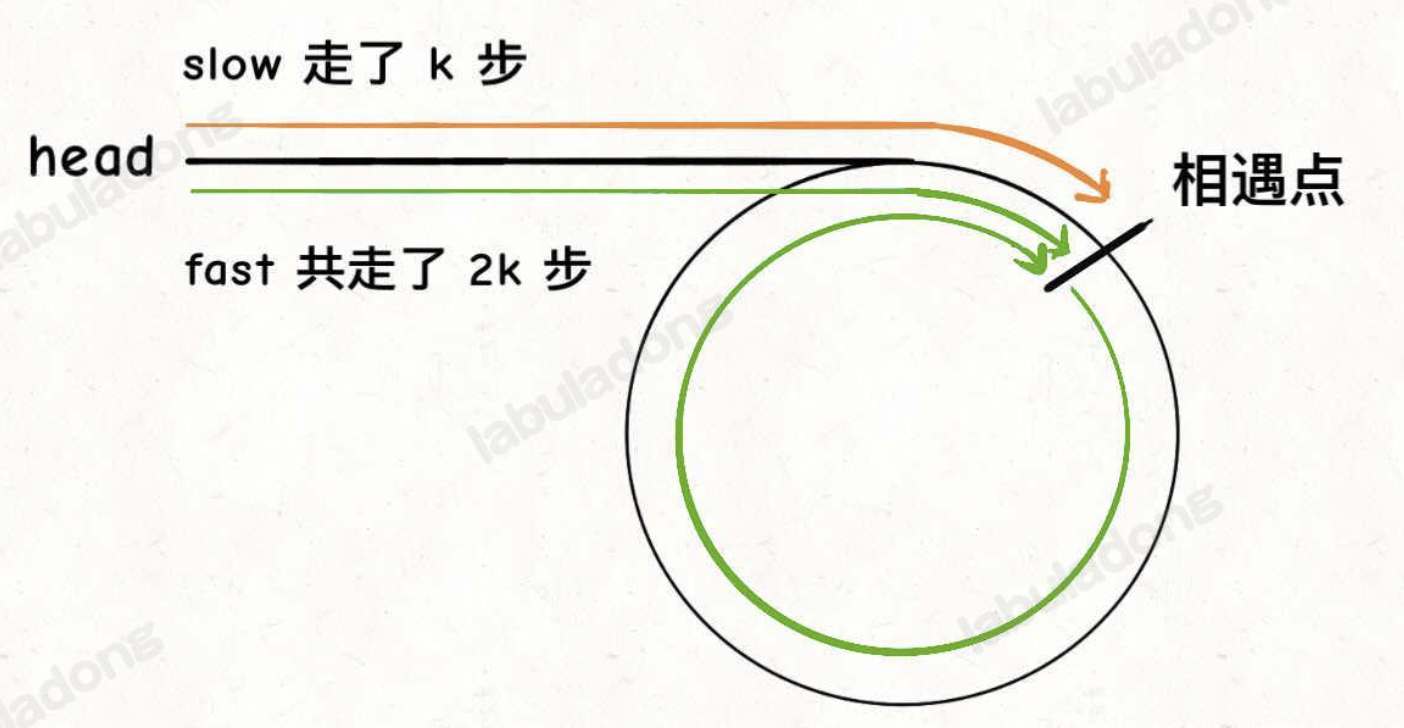

假设head到环起点长度为a; 环起点到相遇点长度为b; 环长度为c. 此时可以列出两个方程:

k = a + b + n * c (n为slow指针绕环的次数)
2k = k + m * c (m为fast比slow多走的次数)

可以得出 a = (m - n) * c - b
此时如果fast节点再前进a的长度, 那么fast节点将回到起点.
head节点再前进a的长度, 那么head节点也可以回到起点.
这样当head和fast重合时就可以得到环的起点.

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode * slow = head;
        ListNode * fast = head;
        while(fast != nullptr && fast->next != nullptr){
            slow = slow->next;
            fast = fast->next->next;
            if(fast == slow) break;
        }   
        if(fast == nullptr || fast->next == nullptr)
            return nullptr;
        slow = head;
        while(slow != fast){
            slow = slow->next;
            fast = fast->next;
        }
        return slow;
    }
};

两链表是否相交

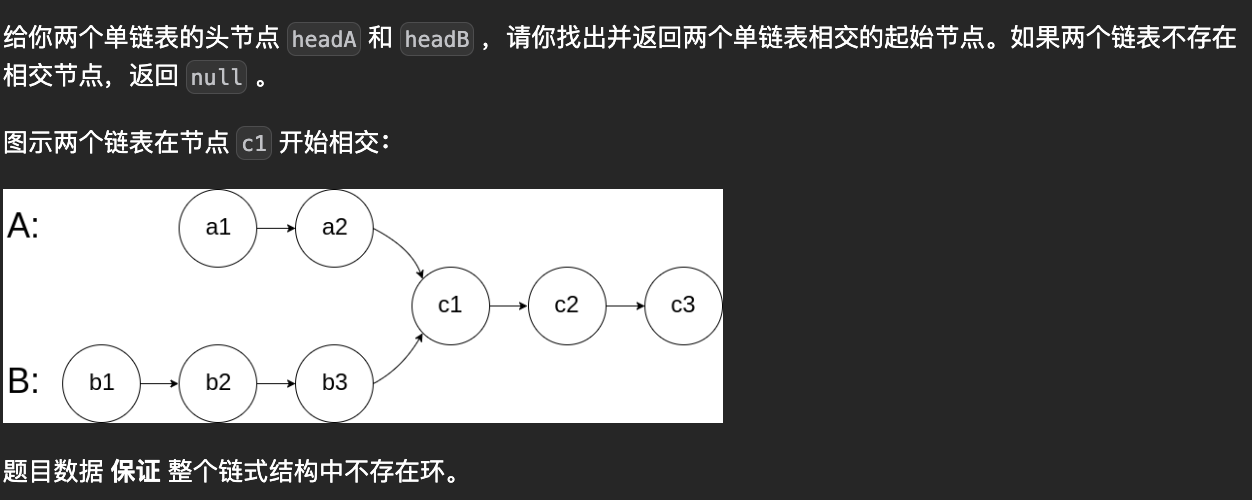
在面对该问题时, 首先的想法是创建一个hash表, 判断二者是否有相同的值.
但这需要分配额外的空间, 如何不使用额外空间来判断是否相交呢?

该问题的难点在于, 两个链表长度不同, 无法在节点之间寻找到对应关系. 指针无法同时走到c1节点,也就无法判断节点是否相同. 但我们可以通过拼接的方式将两个链表的长度变为一致:

当A链表走完后, 继续走B链表.
当B链表走完后, 继续走A链表.

判断二者所指结点是否相同, 相同且不为null: 则相交, 且该节点就是交点; 为null, 则不相交, 同样返回该节点也可以:

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* p1 = headA;
        ListNode* p2 = headB;
        while(p1 != p2){
            if(p1 == nullptr) p1 = headB;
            else p1 = p1->next;
            if(p2 == nullptr) p2 = headA;
            else p2 = p2->next;
        }
        return p1;
    }
};

该问题还可以转换为寻找环起点的问题, 把链表尾节点和其中一个头结点连接后可以生成一个环, 环的起点就是两个链表的交点.