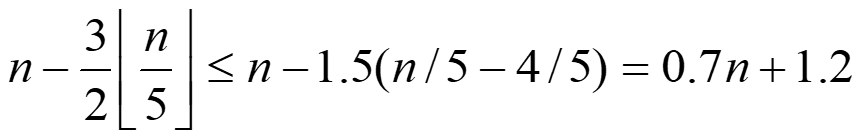Try to be a good coder and emmm… review algorithm class.XD

残缺棋盘

/*A great number of recrusive...XD*/
#include <iostream>
#include <string.h>

using namespace std;

char mylist[100][100];
int ans=0;
void makeup_board(int tr,int tc, int dr, int dc, int size)
{
    int t,s;
    if(size<2)
    return ;
    ans+=1;
    t=ans;
    s=size/2;
    if(dr<tr+s&&dc<tc+s){
        //show that the defective part is in the up-left area
        makeup_board(tr,tc,dr,dc,s);
        mylist[tr+s][tc+s]=t+'A';//emmm, when chessboard big enough, it will beyond 'Z'and there might have amazing thing
        mylist[tr+s-1][tc+s]=t+'A';//and there might have amazing thing.
        mylist[tr+s][tc+s-1]=t+'A';//so,if you want try a big chessboard, please use numbers.
        makeup_board(tr,tc+s,tr+s-1,tc+s,s);
        makeup_board(tr+s,tc,tr+s,tc+s-1,s);
        makeup_board(tr+s,tc+s,tr+s,tc+s,s);
    }else if(dr<tr+s&&dc>=tc+s){//up-right
        makeup_board(tr,tc+s,dr,dc,s);
        mylist[tr+s][tc+s]=t+'A';
        mylist[tr+s][tc+s-1]=t+'A';
        mylist[tr+s-1][tc+s-1]=t+'A';
        makeup_board(tr,tc,tr+s-1,tc+s-1,s);
        makeup_board(tr+s,tc,tr+s,tc+s-1,s);
        makeup_board(tr+s,tc+s,tr+s,tc+s,s);
    }else if(dr>=tr+s&&dc<tc+s){//down-left
        makeup_board(tr+s,tc,dr,dc,s);
        mylist[tr+s][tc+s]=t+'A';
        mylist[tr+s-1][tc+s]=t+'A';
        mylist[tr+s-1][tc+s-1]=t+'A';
        makeup_board(tr,tc,tr+s-1,tc+s-1,s);
        makeup_board(tr,tc+s,tr+s-1,tc+s,s);
        makeup_board(tr+s,tc+s,tr+s,tc+s,s);
    }else if(dr>=tr+s&&dc>=tc+s){
        makeup_board(tr+s,tc+s,dr,dc,s);
        mylist[tr+s-1][tc+s-1]=t+'A';
        mylist[tr+s][tc+s-1]=t+'A';
        mylist[tr+s-1][tc+s]=t+'A';
        makeup_board(tr,tc,tr+s-1,tc+s-1,s);
        makeup_board(tr+s,tc,tr+s,tc+s-1,s);
        makeup_board(tr,tc+s,tr+s-1,tc+s,s);
    }
}
int main()
{
    cout<<"Please input the value of k (used to calculate 2^k)"<<endl;
    int k,size=1,x,y;
    cin>>k;
    for(int i=0;i<k;i++)
    size*=2;
    cout<<"Please input the defective location (x,y) from 1~2^k"<<endl;
    cin>>x>>y;
    memset(mylist,'#',sizeof(mylist));
    makeup_board(0,0,x-1,y-1,size);
    for(int i=0;i<size;i++){
        for(int j=0;j<size;j++)
        cout<<mylist[i][j]<<" ";
        cout<<endl;
    }
    return 0;
}

---

Merge Sort

#include <iostream>

using namespace std;

void meger(int *mylist,int left,int mid, int right)
{
    int i=left, j=mid+1;
    int counter=0;
    int * ans =new int [right-left+1];
    while(i<=mid&&j<=right)
    {
        if(mylist[i]<=mylist[j]){
            ans[counter++]=mylist[i++];
        }
        else 
        ans[counter++]=mylist[j++];
    }
    while(i<=mid)
    {
        ans[counter++]=mylist[i++];
    }
    while(j<=right)
    ans[counter++]=mylist[j++];

    for(int i=left,k=0;i<=right;i++,k++)
    mylist[i]=ans[k];
}

void meger_sort(int *mylist,int left, int right)
{
    if(left<right)
    {
        int mid=(left+right)/2;
        meger_sort(mylist, left,mid);
        meger_sort(mylist,mid+1,right);
        meger(mylist,left,mid,right);
    }
}

int main()
{
    int lenght, *mylist, *ans;
    cin>>lenght;
    mylist= new int[lenght];
    for(int i=0;i<lenght;i++)
    cin>>mylist[i];
    meger_sort(mylist,0,lenght-1);
    for(int i=0;i<lenght;i++)
    cout<<mylist[i]<<" ";
    cout<<endl;
    return 0;
}

---

金块问题

Max-Min(A[1,n], max, min)

if n==1  max<- min<- a[1]; return ;

if n==2 比较a[1] a[2]大小

else

m<- n/2

Max-Min (A[1,m], max1 , min1 )

Max - Min(A[m+1, n] ,max2 , min2 )

max <- max(max1, max2)

min< - min (min1 , min2)

return ;

/*Easy code without recursive*/
#include <iostream>

using namespace std;

int Minmax(int *mylist,int n, int &maxx, int &minn)
{
    if(n<1)
    return 0;
    if(n==1)
    {
        maxx=minn=0;
        return 1;
    }
    int start;
    if(n%2){
        maxx=minn=0;
        start=1;
    }else{
        mylist[0]>mylist[1]?maxx=0,minn=1 : minn=0,maxx=1;
        start=2;
    }
    for(int i=start;i<n;i+=2){
        if(mylist[i]>mylist[i+1]){
            if(mylist[i]>mylist[maxx])
                maxx=i;
            if(mylist[i+1]<mylist[minn])
                minn=i+1;
        }else{
            if(mylist[i+1]>mylist[maxx])
            maxx=i+1;
            if(mylist[i]<mylist[minn])
            minn=i;
        }
    }
    return 1;
}

int main()
{
    int len;
    cout<<"Input the length of array"<<endl;
    cin>>len;
    int *mylist=new int [len];
    cout<<"Input the elements of array"<<endl;
    for(int i=0;i<len;i++)
    cin>>mylist[i];
    int maxx=0,minn=0;
    if(Minmax(mylist,len,maxx,minn)){
        cout<<"the biggest is ";
        cout<<mylist[maxx]<<" the min is "<<mylist[minn]<<"\n";
    }
    return 0;
}

n==2^k^时复杂度分析

     0, n==1

C(n)=    1, n==2

     2xC(n/2) + 2 , 其他

C(n)=（3n/2）-2

主项法：a=2，b=2，logba=1，n^1^=n，f(n)==2==θ(1)

C(n)=θ(n)

---

快速排序

#include <iostream>

using namespace std;

int partation(int * mylist, int left ,int right)
{
    int povit=mylist[left];
    while(left<right){
        while (left<right&&mylist[right]>=povit)
            right--;
        mylist[left]=mylist[right];
        while (left<right&&mylist[left]<=povit)
            left++;
        mylist[right]=mylist[left];
    }
    mylist[left]=povit;
    return left;
}

void quicksort(int* mylist,int left, int right)
{
    if(left>right)
    return ;
    int j=partation(mylist,left,right);
    quicksort(mylist,left,j-1);
    quicksort(mylist,j+1,right);
}

int main()
{
    int mylist[6]={0,4,5,3,2,6};
    quicksort(mylist,0,5);
    for(int i=0;i<6;i++)
    cout<<mylist[i]<<" ";
    cout<<endl;
    return 0;
}

时间复杂度分析

最坏情况下

Tmax(n)=O(1)，n<=1

   =T(n-1)+O(n)=O(n^2^)，n>1。即产生的区域分别包括n-1和n个元素

最好情况下

Tmin(n)=O(1)，n<=1

   =2T(n/2)+O(n)=O(nlogn)，n>1。即产生的区域每次都为n/2

平均时间复杂度为θ(nlogn)

证明：

每轮快排将数组分成两部分，用S代表左数据段元素个数，右数据段元素个数为n-s-1，S取0~n-1中任何数的概率为 1/n

T(n)=1/n Σs=0^n-1^ (T(s)+T(n-s-1)) + cn=2/n Σs=0^n-1^ T(S) + cn

由nT(n)-(n-1)T(n-1)=2T(n-1)+O(n)得

T(n)=（1+1/n)T(n-1)+ O(n)

归纳得T(n)=θ(nlogn)

---

选择问题

对给定序列，选出其中第k小的元素

该问题可在O(nlogn)时间内解决，方法为先排序，再取出a[k-1]元素

若用快速排序，可取得较好的平均复杂度，但最坏复杂度为O(n^2^)

朴素算法（使用快排）

#include <iostream>

using namespace std;

int partation(int * mylist, int left ,int right)
{
    int povit=mylist[left];
    while(left<right){
        while (left<right&&mylist[right]>=povit)
            right--;
        mylist[left]=mylist[right];
        while (left<right&&mylist[left]<=povit)
            left++;
        mylist[right]=mylist[left];
    }
    mylist[left]=povit;
    return left;
}

int quicksort(int* mylist,int left, int right,int k)
{
    if(left==right)
    return mylist[left];
    int j=partation(mylist,left,right);
    if(k==j-left+1)
    return mylist[j];
    if(k-j+left<1)
    return quicksort(mylist,left,j-1,k);
    else 
    return quicksort(mylist,j+1,right,k-j+left-1);
}

int main()
{
    int len;
    cin>>len;
    int *mylist=new int [len];
    for(int i=0;i<len;i++)
    cin>>mylist[i];
    cout<<quicksort(mylist,0,len-1,3)<<endl;
   
    return 0;
}

复杂度分析：

若left和right总是同样大小，或者相差不超过一个元素，那么递归式如下

T(n)=T(n/2)+cn， n>1

​ d， n<=1

若n==2^k^，可通过迭代方法得到T(n)=θ(n)

即选择较好的分点，可以得到较好的性能。

中间的中间

若仔细地选择支点元素，则最坏情况下的时间开销也可以变成θ(n)

规则：

首先将数组a中的n 个元素分成n/r 组，r 为某一整常数。

除了最后一组外，每组都有r 个元素。然后通过在每组中对r 个元素进行排序来寻找每组中位于中间位置的元素。

最后对所得到的n/r 个中间元素，递归使用选择算法，求得”中间之中间”作为支点元素

当使用中间的中间规则选取支点时，下定理成立

若r=5，且a 中所有元素都不同，那么当n≥24时，有max{| left |, | right | }≤3n/ 4

*有 ⌈1/2 * ⌊n/5⌋ ⌉ 多个中间元素不大于mm。*

大于mm元素的数目有上界

故，当n>=24时，0.7n+1.2≤3n/4

r==5时

T(n) ≤ T(n/5) + T(3n/4) +Θ(n)

归纳法可证明当n≥24时有t(n)≤20cn

r=9, 当n≥90时，有max{ |left|,|right|}≤7n/8

问：用第K小做支点的快速排序时间复杂度•在快速排序算法中，如果我们先调用最坏情形时间复杂度O(n)的选择算法找出第n/2小元素并以此为支点(pivot)对要排序的数组进行分划，则改进后的快速排序算法的最坏情形时间复杂度T(n)是什么？假定n=2k，列出T(n)满足的递归方程并分析.

解答：用第n/2小的元素做支点，把数组分成均等的两半，同时，分化的最坏情形时间代价为O(n)=cn，则改进快速排序算法的最坏时间复杂度为T(n)=2T(n/2)+cn。符合主定理case2，T(n)=Θ(nlogn)。假定n=2k，T(n)=2T(n/2)+cn=2kT(1)+k⋅cn=Θ(n+nlogn)=Θ(nlogn)。

求逆序个数

#include <iostream>

using namespace std;

int sum=0;


void mergecount(int *mylist,int l, int mid,int r, int *temp)
{
    int p1=l, p2=mid+1, index=0;
    while(p1<=mid&&p2<=r){
        if(mylist[p1]<mylist[p2]){
            temp[index++]=mylist[p1++];
        }else{
            temp[index++]=mylist[p2++];
            sum+=mid-p1+1;
        }
    }
    while(p1<=mid){
        temp[index++]=mylist[p1++];
    }
    while(p2<=r){
        temp[index++]=mylist[p2++];
    }
    for(int i=0;i<r-l+1;i++)
    mylist[l+i]=temp[i];
}
void mergesort(int *mylist, int l, int r,int *temp)
{
    if(l<r){
        int mid=(l+r)/2;
        mergesort(mylist,l,mid,temp);
        mergesort(mylist,mid+1,r,temp);
        mergecount(mylist,l,mid,r,temp);
    }
}

int main()
{
    int n;
    cout<<"Input the number of data"<<endl;
    cin>>n;
    int *temp=new int [n];
    int *mylist=new int[n];
    cout<<"Input datas"<<endl;
    for(int i=0;i<n;i++)
    cin>>mylist[i];
    mergesort(mylist,0,n-1,temp);
    cout<<sum<<endl;
    return 0;
}