今天刷洛谷基础题看到一个很好的题，分享一下。

​ 原题链接

题目描述

对于一个 n 个顶点的凸多边形，它的任何三条对角线都不会交于一点。请求出图形中对角线交点的个数。

例如，6 边形：

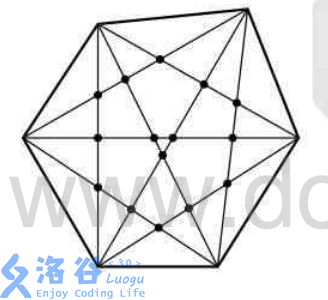
输入格式

输入只有一行一个整数 nnn，代表边数。

输出格式

输出一行一个整数代表答案。

输入输出样例

输入 #1   输入#2

3       6

输出#2     输入#2

0       15

说明与提示

• 对于 50%50 %50% 的数据，保证 3≤n≤100。
• 对于 100%100 %100% 的数据，保证 3≤n≤10^5。

题解

首先看题目中一句任何三条对角线都不会交于一点，所以给定一个交点，可以确定两条对角线——也就意味着确定了四个角

所以这道题就变成了一个排列问题

即求Cn4的组合数问题 ：就是求 n * (n-1) * (n-2) * (n-3) /24

这时大家可能会想 ”啊，这个题目这么简单，怎么会有人拿他出来写博客！”

所以你就写出了下面的代码

#include <iostream>

using namespace std;

int n;

int outcome;

int main()
{
    cin>>n;
    outcome=n*(n-1)*(n-2)*(n-3)/24;
    cout<<outcome<<endl;
    return 0;
}

结果

再仔细阅读下题目，你会发现这道题会爆数据的…

所以你把int 全部换成了long long 或者unsigned long long ，并沾沾自喜，这么简单不会真有人拿出来写博客吧！

结果你又发现出现了两个WA…（手动狗头）

这时你想到，我可以写高精求组合数啊

这无疑是一种很好的解题方法，但对于这样一道入门题来说，未免太…

所以给出了一个很妙的写法

那就是把 n * (n-1) * (n-2) * (n-3) /24写成 n * (n-1)/2 *(n-2) /3 *(n-3)/4

#include <iostream>

using namespace std;

unsigned long long n;

unsigned long long outcome;

int main()
{
    cin>>n;
    outcome=n*(n-1)/2*(n-2)/3*(n-3)/4;
    cout<<outcome<<endl;
}

现在来分析一下为什么这样写是对的。

首先n * (n-1)中一定有一个是2的倍数，所以可以被2整除

n * (n-1) *(n-2)中一定有一个是3的倍数，所以可以被3整除

n * (n-1) * (n-2) * (n-3) 中一定有一个是4的倍数，所以可以被4整除

emmmmmmmmmmm，就差不多是这样了

溜了溜了，上课去。